Uno è strano perché solo, pensò il due planando a volo./ Siamo in tre concluse il terzo, sorridendo senza sforzo./ Mister quattro di soppiatto in silenzio si accostò./ Disse il cinque che seguiva: “fammi posto!” e un calcione gli sferrò./ “Sei un bel tipo” disse quello, rimirandosi allo specchio, sei il più bello, per di più sei pure tosto./ Occhio al sette aggiunse l’otto, con lo sguardo spaventato./ Mentre il nove già premeva, stanco serio e impomatato./ ‘Fuori tutti, valgo doppio’ urla il dieci nella testa del piccino./ Ma quel discolo lo afferra, lo divide per benino poi lo butta nel camino./ Brucia il numero fatato: tutto e nulla ha numerato./ Primo o ultimo che sia, è finita la magia./ Non aveva, del pupetto, calcolato l’inventiva che si sa, è cosa viva.
I numeri sembrano nati per le filastrocche – anche se diffidano della rima – perché sono disponibili a qualsiasi gioco e perché c’è sempre una regola, la regola del gioco, che ne amministra i comportamenti. I numeri si assoggettano volentieri ad essere una quantità e diventare subito ritornello mettendosi in fila, moltiplicandosi, dividendosi, sommandosi e sottraendosi, ma si lasciano trasformare volentieri in qualità: l’uno è magro, allampanato, con il naso aquilino, il tre è così goloso che non gli basta una pancia sola, il nove è un tipo tutta testa. I numeri sono tutti maschi, per questo qualcuno li trova aridi. D’altra parte l’economia che impiega i numeri per fare i suoi conti è una cosa da uomini, e la sua compagnia più fidata è la guerra cui capita spesso di scambiare i soldati per numeri. Cosa che, per rendergli il favore, fa anche la web economy, trasformando le persone in consumatori numerati il cui valore matematico è elaborato e reso fruttifero dagli algoritmi.
Ma i numeri amano le filastrocche proprio perché ci tengono assai a convincere i bambini che non sono delle persone senza cuore, non sono soldati e non sono algoritmi.
Il dottor Williams Carlos Williams nel suo fondamentale Nelle vene dell’America ricorda come a un critico poeta che rinfacciava ad Edgar Allan Poe di scrivere cose “dove il cuore manca, sloggiato dalla mente”, questi aveva replicato che “la più alta categoria dell’intelletto immaginativo è sempre eminentemente matematica”.

Illustrando le fasi di composizione del suo più celebre poema, Il corvo, Poe nel saggio La filosofia della composizione apparso nel 1846 sul «Graham’s Magazine» scrisse: “È mia intenzione rendere evidente come nessun momento nella sua composizione sia rapportabile o a un incidente o a un’intuizione; che il lavoro è proceduto passo passo, fino al suo completamento, con la precisione e la rigida consequenzialità di un teorema matematico”
Le filastrocche con i numeri mettono alla prova la metrica e l’immaginazione, cioè l’ordine e il caos.
Per questo vi si sono esercitati un numero infinito (secondo la dimostrazione di Euclide) di letterati.
Quella scritta da Gianni Rodari per le Favole al telefono, nel 1962, è esemplare:
A inventare numeri
– Inventiamo dei numeri? - Inventiamoli, comincio io. Quasi uno, quasi due, quasi tre, quasi quattro, quasi cinque, quasi sei.
– È troppo poco. Senti questi: uno stramilione di biliardoni, un ottone di millantoni, un meravigliardo e un meraviglione.
– Io allora inventerò una tabellina:
tre per uno Trento e Belluno
tre per due bistecca di bue
tre per tre latte e caffè tre per quattro cioccolato tre per cinque malelingue tre per sei patrizi e plebei tre per sette torta a fette tre per otto piselli e risotto tre per nove scarpe nuove tre per dieci pasta e ceci.– Quanto costa questa pasta? - Due tirate d’orecchi”. - Quanto c’è da qui a Milano? - Mille chilometri nuovi, un chilometro usato e sette cioccolatini. - Quanto pesa una lagrima? - Secondo: la lagrima di un bambino capriccioso pesa meno del vento, quella di un bambino affamato pesa più di tutta la terra. - Quanto è lunga questa favola? - Troppo.
– Allora inventiamo in fretta altri numeri per finire. Li dico io, alla maniera di Modena: unci dunci trinci, quara quarinci, miri miminci, un fan dès.
– E io li dico alla maniera di Roma: unzi donzi tenzi, quale qualinzi, mele melinzi, riffe raffe e dieci.

La filastrocca dedicata ai numeri da Roberto Piumini invece ci dice che sono loro, i numeri, i custodi occulti dello storytelling, l’atto di convertire i concetti in narrazione. Ogni bambino sarà curioso di apprendere cosa si può imparare sulla natura del numero sette sapendo che indossa le ghette.
Uno era a digiuno, due si mangiò un bue. Tre è un grande re, quattro porta lo scettro. Cinque sa molte lingue, sei sa i fatti miei. Sette porta le ghette, otto porta il cappotto. Nove è a far le prove, dieci son pochi ceci.

Quando parliamo di matematica possiamo fingere tutti di sapere di che cosa stiamo parlando: di numeri. Non proprio.
La matematica è ben più delle sole operazioni aritmetiche e purtroppo per quelli come me che fanno fatica a destreggiarsi con una sola “esistono molte matematiche; l’aritmetica, la fisica matematica, l’algebra, la geometria, l’analisi e la statistica” e ciascuna risponde a domande diverse, sottostà a leggi diverse e si comporta con un’ostinata autonomia di giudizio “anche se in molti casi lo studio delle strutture matematiche astratte ha rivelato sorprendenti affinità tra ambiti disparati, lasciando intravedere le linee di una conoscenza unitaria.” Così ci istruisce Paolo Zellini nel suo La matematica degli dei e gli algoritmi degli uomini Adelphi, Milano 2016.

Se si pensa poi che la matematica sia una borsa degli attrezzi adatta a misurare il mondo, non dobbiamo dimenticare a casa la geometria. Secondo Galileo Galilei, come scrive nel Saggiatore pubblicato a Firenze nel 1623, l’universo è un grandissimo libro che non si può capire se non si conosce la lingua in cui è scritto: “Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi, ed altre figure geometriche, senza i quali mezi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro laberinto”.”
La filosofa francese Simone Weil (1909-1943) ricordava che Platone aveva affisso sulla porta dell’Accademia questo diktat: “Nessuno entri qui se non è geometra” e diceva: “Dio è un perpetuo geometra”.
E questa faccenda della geometria non è cosa da poco, poiché misurare il mondo è metterlo in equilibrio: “Agli occhi dei Greci la misura, l’equilibrio, la proporzione e l’armonia costituivano il principio stesso della salvezza dell’anima, perché i desideri hanno come oggetto l’illimitato”. Nell’eliminazione dell’illimitato risiede la giustizia, e l’«uguaglianza geometrica» diventa allo stesso tempo suprema legge dell’universo e condizione per la salvezza dell’anima. Analizzando poi l’Iliade come poema della forza, Weil intensifica la relazione tra morale e matematica: “Le idee di limite, di misura, di equilibrio, che dovrebbero determinare la condotta di vita, ormai hanno solo un impiego servile nella tecnica. Noi siamo geometri soltanto davanti alla materia; i Greci furono geometri innanzitutto nell’apprendimento della virtù”.

Se è così non ci si dovrebbe industriare di rendere il più facilmente accessibile ai piccoli quest’alfabeto fondamentale per leggere il libro della natura, apprezzare le opere dell’uomo e rinsaldare la propria virtù? Non vorrei che l’ora di matematica diventasse un’ora di religione, seppure laica, ma nemmeno fosse l’ora di ginnastica per un nemico delle flessioni e del quadro svedese.
Non so se, come dice Platone, sia stato davvero Urano, il dio preposto a configurare nel movimento degli astri le leggi dei numeri e delle proporzioni, a donarci la matematica ma le Muse avrebbero dovuto senz’altro impegnarsi di più nel renderla compiacente.
Il fratello di Simone Weil, André, era un valente matematico e il suo campo non era di sicuro l’aritmetica ma lo scetticismo con cui risponde alle richieste della sorella di saperne di più sul suo lavoro, è allarmante:
Quanto a parlare delle mie ricerche o di qualsiasi altra ricerca matematica ai non-specialisti, tanto varrebbe spiegare una sinfonia a dei sordi, mi sembra. Lo si può fare, certo. Ci si serve di immagini, si parla di temi che si rincorrono, s’intrecciano, si coniugano o si separano, di tristi armonie o di trionfanti dissonanze: ma una volta finito, che cosa si è prodotto? Frasi, o tutt’al più un componimento bello o brutto, che non ha nulla a che fare con ciò che si voleva descrivere. Da questo punto di vista la matematica non è altro che un’arte; una sorta di scultura in una materia estremamente dura e resistente (come certi porfidi che a volte usano, credo, gli scultori). (…) Ma l’opera che si fa è opera d’arte, e in quanto tale inspiegabile (in essa sola risiede la sua spiegazione)

Nell’immagine un busto ritraente Platone rinvenuto nel 1925 nell’area sacra in Largo Argentina a Roma.
Copia conservata nei Musei Capitolini di un’opera attribuita al greco Silanion
Davanti a tanta severità meglio ridurre le ambizioni e avvicinare la matematica attraverso il gioco o con i trucchi dell’illusionista, anteporre alle forme universali e astratte la vita confortante delle relazioni e dell’esperienza. La scuola deve dare a ciascun soggetto i mezzi per pensare il mondo e gli alfabeti per leggerlo e interpretarlo in modo singolare. Ma non è detto che questo soggetto debba essere lasciato solo dinanzi a quel suo ostico oggetto. Il gioco, che è pratica di condivisione, esperienza comune, ha l’aria di essere un ottimo strumento per superare l’angoscia del rapporto io-numeri. La pensano così anche quelli di «weDraw», un progetto europeo coordinato dall’Istituto italiano di tecnologia (Iit), che va elaborando un sistema multisensoriale per l’insegnamento dell’aritmetica e della geometria. Il primo passo nell’applicazione di questo metodo è la valutazione attraverso vari test delle competenze degli allievi per poterne monitorare i progressi.
La sperimentazione successiva è condotta con giochi in cui viene fatto uso di sensori, di uno schermo e di uno strumento che permette di manovrare un oggetto virtuale ed esplorare un ambiente mediante sensazioni tattili. L’obiettivo è di far comprendere meglio, attraverso l’uso di vista, tatto e udito, alcuni concetti astratti come quello di rotazione mentale, frazione, equivalenze, percentuali, trasformazioni isometriche e piani cartesiani.
Dice Gualtiero Volpe, ingegnere informatico impegnato nel progetto «weDraw»
Stiamo creando giochi in grado di stimolare i sensi dei bambini, associandoli a concetti matematici. Studi scientifici condotti con i colleghi dell’Iit suggeriscono che i bimbi associano in modo naturale i suoni acuti ad angoli di piccole dimensioni, quelli gravi ad angoli grandi. Così abbiamo ideato un gioco nel quale va disegnata una casa con le braccia, riproducendo man mano i vari angoli e ascoltando i suoni corrispondenti. Adesso vogliamo capire se il bambino è annoiato e stressato e regolare le difficoltà di conseguenza, ma anche farli giocare insieme” (La Repubblica, 13 giugno 2018).
In questo video la sonorizzazione dei movimenti è impiegata per supportare la comprensione della matematica. Nella prima demo si mostra come creare angoli usando il movimento delle braccia. Diversi angoli sono associati a diverse note musicali: suoni acuti sono usati per sonorizzare angoli acuti e suoni gravi per angoli ottusi. Nella seconda è espressa la relazione matematica fra pattern ritmici creati attraverso il battito delle mani e le frazioni. Nella terza la frazione diventa corpo: l’apertura delle braccia e delle gambe controlla il numeratore e denominatore della frazione, rispettivamente
Nel frattempo, mettendo da parte l’hi-tech e tornando alla tecnologia di Gutenberg, si possono riaprire le pagine dell’Agenda Casa Serena 1989 e leggere cosa scriveva e proponeva il maestro Alberto Manzi, nel suo Per non farla odiare!… (la matematica).
Dell’avversione per la matematica spesso la causa è proprio la scuola che “preoccupata di far fare presto addizioni e sottrazioni, divisioni e moltiplicazioni, dimentica che occorre innanzitutto che il bambino giunga al «concetto di numero» dopo aver «lavorato» con delle quantità, dopo aver «ragionato» sulle cose; e non si può ragionare sulle cose se non si impara a «vedere» le cose, a mettere in relazione ciò che si vede con le cose… Ci si dimentica che il linguaggio è l’altro elemento importante per la formazione dei concetti; ma se non si fanno cose, su cosa si parla? Come preciso il linguaggio se non ho… da precisare qualcosa?”.



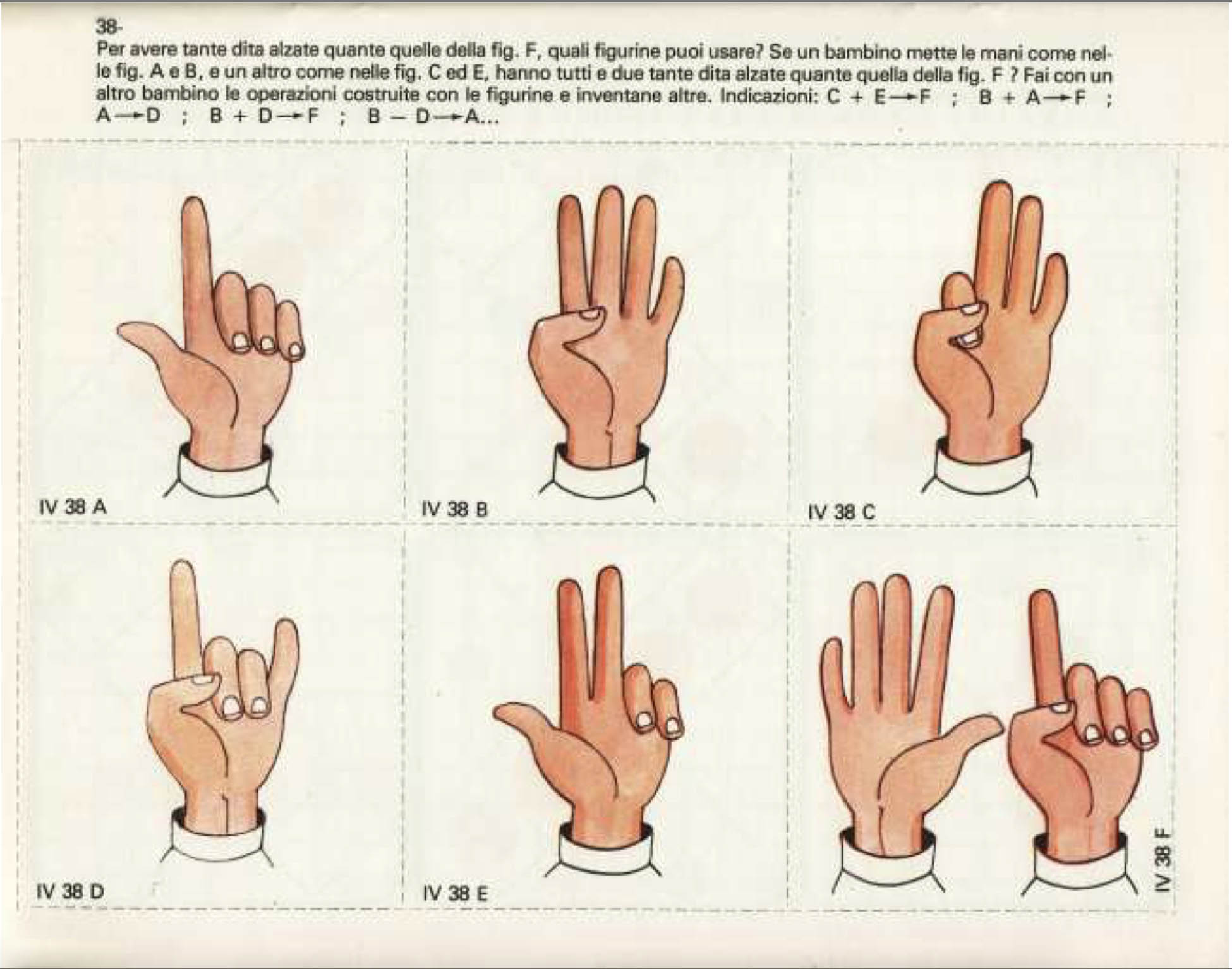
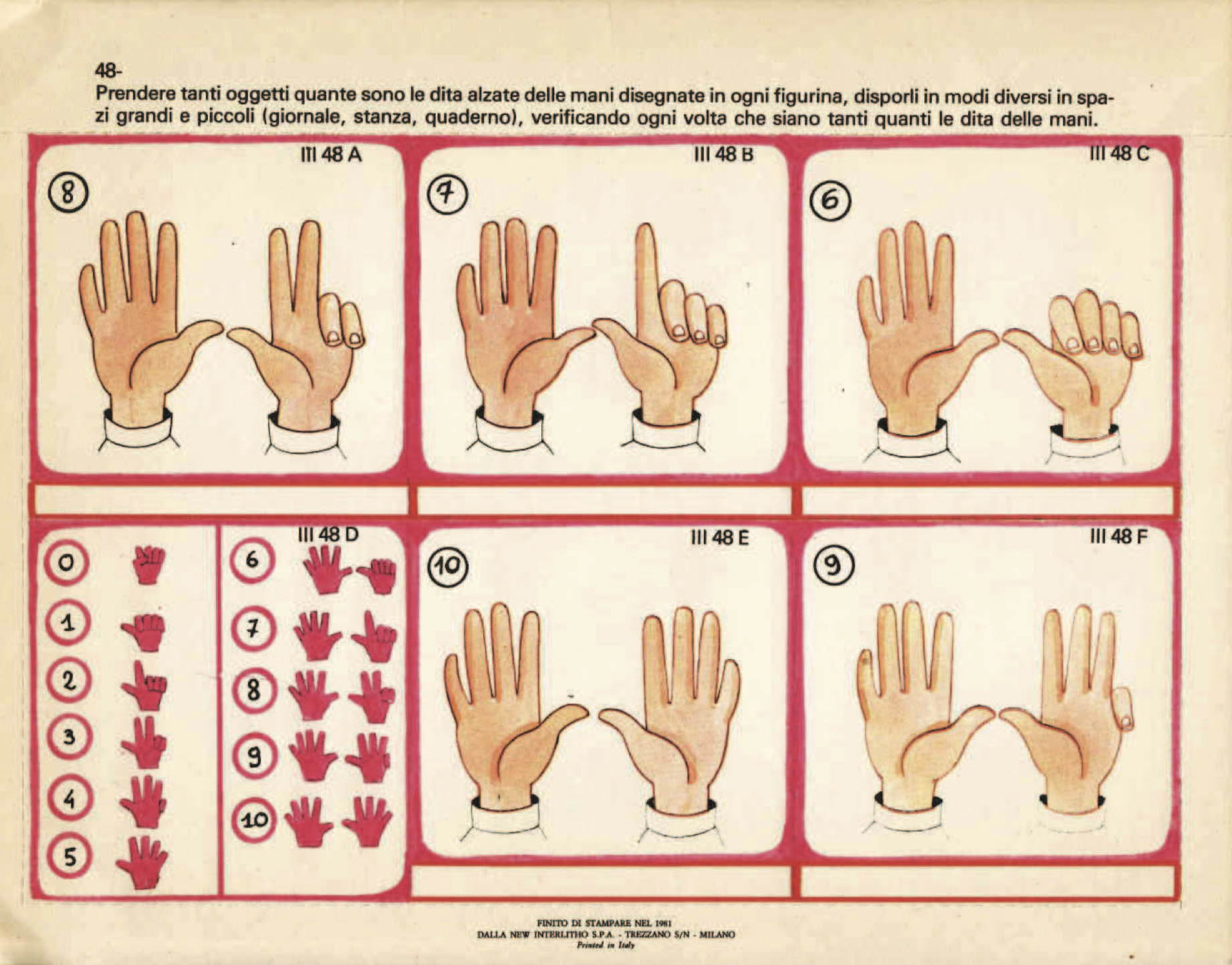
 Queste e le immagini seguenti sono tratte da diversi numeri dei quaderni di lavoro inventati da Alberto Manzi con il titolo Fare e Disfare
Queste e le immagini seguenti sono tratte da diversi numeri dei quaderni di lavoro inventati da Alberto Manzi con il titolo Fare e DisfareL’assonanza con le metodologie multisensoriali più recenti apparirà ancora più evidente scartabellando nelle schede organizzate come appuntamenti quotidiani sul calendario: la classificazione s’impara mettendo insieme una figura scomposta e ragionando sull’ordine dato ai pezzi (simmetria, significato, numerazione). Allo stesso modo un qualsiasi gruppo di oggetti sarà utile per spiegare il concetto di unità coerente. E la classificazione per forme (ordine, relazione, insieme) potrà sì comportare l’uso di triangoli, quadrati, cerchi, sfere e cubi, ma meglio sarà servirsi di tovaglioli, scatole, palle, barattoli ecc. Per combinare associazione e spazializzazione ecco un gioco dell’oca in cui simboli e oggetti si attraggono e il percorso aiuta a precisare l’uso di alcune parole: prima… dopo… tra il… e il ecc. Nei Quaderni Fare e Disfare (Quaderni di lavoro. Esercizi e giochi da fare e disfare per capire e riflettere sulle cose, sulle parole, sui numeri) il maestro ha profuso invenzioni grafiche e testuali, narrazioni, indovinelli, problemi, immagini tutti volti a giocare (dunque a imparare, così come Wittgenstein inseguiva i fondamenti della filosofia con i giochi linguistici) con le quantità, le proporzioni, le dimensioni, le relazioni, le sequenze, le analogie, le corrispondenze, le equivalenze che fanno del mondo un mistero decifrabile, comprensibile in parte, ma innanzitutto vitale. A premessa di una serie di quaderni-schede per sollecitare al ragionamento e all’osservazione Manzi puntualizzava di aver sempre tenuto presente nel realizzare quel lavoro “che occorre insegnare a pensare, piuttosto che insegnare dei pensieri”. I pensieri in effetti sono una proprietà legittima della mente, che ne è gelosa; sono, una volta pensati, già separati da noi. Pensare invece è un’azione che si trova a suo agio con tutto il corpo, con tutti i sensi. Si pensa toccando, guardando, perfino assaggiando, muovendosi, ascoltando.




La matematica trae enorme giovamento, credo, non solo da questa descrizione del pensiero come attività organica, ma anche dall’essere affrontata come un oggetto concreto, costituito da materia, relazioni e storie.
La parola relazione con la sua evocazione di affetti, presenze, confronto, è centrale in questi materiali quanto la parola proporzione ed è senz’altro suggestivo che ancora Simone Weil abbia scritto sulla proporzione, all’origine del pensiero matematico dei greci, come di uno strumento etico.
Non è facile concepire ed esprimere in che cosa sia esattamente consistito il ruolo della proporzione. Per quanto riguarda l’arte, la proporzione permette al pensiero di cogliere e ordinare in un solo colpo la diversità. Quando si fa uso della proporzione assennatamente – vale a dir in modo da lasciar sussistere il sentimento della diversità – il pensiero si trova nella situazione più felice, che consiste nel sentirsi a casa propria in mezzo alla materia. Si potrebbe definire lo scopo dell’arte il condurre l’anima a sentirsi a casa propria nel luogo del suo esilio. Ma gli oggetti fabbricati non bastano; il pensiero desidera poter percepire il mondo stesso come un’opera d’arte; si tratta quindi non più di stabilire, ma di trovare delle proporzioni. Quante più se ne percepiscono, tanto più l’universo diventa il contrario di un incubo (…). Non si può ammirare un’opera d’arte senza credersene in qualche modo l’autore; ammirare l’universo come opera d’arte equivale ad assimilarsi in qualche modo a Dio. Le matematiche sono utili a questo scopo in quanto scienza della natura [ma anche scienza del gioco]. Appare chiaro che ritrovare alcuni rapporti semplici in apparenze mutevoli e diverse, in cui l’uomo si smarrisce, procura una felicità di questo genere. Un rapporto che si presenta identico in cose diverse è la nozione stessa di proporzione.
Non è un paradosso affermare che le proposte di Alberto Manzi per insegnare ai più piccoli i concetti fondamentali della matematica degli insiemi rispondessero a quest’ambizione: “ritrovare alcuni rapporti semplici in apparenze mutevoli e diverse”.
Si tratta di un’ambizione così universale e così connaturata alla matematica che la proporzione è protagonista anche nel formidabile film d’animazione Paperino nel mondo della matemagica (Walt Disney, 1959, accreditato a ben quattro registi: Les Clark, Joshua Meador, Wolfgang Reitherman, Hamilton Luske), perché dalla sezione aurea in poi tutto è proporzione. La solerte voce fuori campo catechizza Paperino: “il rettangolo aureo era il principio matematico della bellezza”. Segue l’analisi geometrica del Partenone, della cattedrale di Notre Dame e della Gioconda (ma Paperino si entusiasma solo per le proporzioni di una ballerina quasi classica). La sezione aurea misura con dovizia la natura e campeggia il motto della società pitagorica della stella a cinque punte “tutto è disposto secondo numeri e forme matematiche” (conchiglie, fiori, piante, animali, ma anche la giostra). Lo spirito guida è quello dell’avventura, ma non ci si dimentica che Pitagora è il padre tanto della matematica che della musica, o padre di questa in quanto genitore di quella (Paperino ha smesso di stare attento e si butta in una jam session con pitagorici in peplo e contrabbassisti neri). Nemmeno la sceneggiatura l’avesse scritta il maestro Manzi tutto è concretezza, una fantasmagoria di cosità in meravigliosa corrispondenza formale. I fondamenti geometrici del gioco sono disvelati da scacchi (Alice attraverso lo specchio e la partita con pedoni, cavalli e regine molto, troppo umani) baseball, basket fino al gioco della campana e al biliardo (la spiegazione matematica del sistema di rapporti tra angoli naturali e posizione della stecca con relativo calcolo per sottrazioni del punto da colpire è meravigliosa e ammaliante). Il passaggio dal cono agli ingranaggi, al faro, al trapano, alla molla, all’orologio, al telefono, al tamburo, allo stantuffo, è un virtuosismo che illumina la trama semplice dell’infinitamente complesso.
Walt Disney Paperino nel mondo della matemagica 1959.
Un mondo pieno di musica quello della matematica, da Pitagora al Jazz.

qualcosa da comunicare attraverso questo vasto linguaggio matematico…”
D’altra parte c’è chi ha pensato a un metodo per insegnare la matematica con la musica, vedi l’ebook di A. Bianchi, C. Cuomo, G. Curti, D. Lentini, N. Magnani, R. Vagni Doremat – La musica della matematica. Insegnare e imparare la matematica con la musica, Modena 2015
Ma se mettiamo da parte Paolino Paperino il cinema ha ribadito che la matematica è roba da geni, che oltreché geni spesso sono nevrotici, instabili, sofferenti, sociopatici. A causa della matematica?
Nel loro caso l’espressione genio e sregolatezza suona decisamente ironica. Basta pensare a Will Hunting di Gus Van Sant, A Beautiful Mind di Ron Howard o The Imitation Game di Morten Tyldum.
Naturalmente Hollywood ci ha provvisto anche di un genio molto più innocente e simpatico, il piccolo Erasmo Leaf figlio di un professore di filosofia, cultore delle arti, che ha in odio la matematica sino a quando non scopre come le eccezionali abilità di calcolo del piccino permettano grandi vincite scommettendo sui cavalli. Il denaro guadagnato dalla matematica servirà a Erasmo per conoscere il suo mito, Brigitte Bardot, e al padre a devolvere ricchezza alle belle arti.

Anche suo padre, James Stewart, dovrà convincersi che la felicità non è solo patrimonio delle belle arti
Comunque che la matematica debba travestirsi, romanzarsi o musicarsi, per suscitare l’interesse e conservare l’attenzione dei ragazzi è convinzione antica e non solo prassi disneyana. Così la matematica diventa gioco, enigma, indovinello. Alla corte di Carlomagno, nel 781, Alcuino di York si era impegnato a rendere acuta la mente dei giovani (Giochi matematici alla corte di Carlomagno, 2005) interrogandoli con quesiti che ancora oggi stuzzicano irresistibilmente la più ingenua curiosità: Un bue che ara tutto il giorno, quante impronte lascia nell’ultimo solco?
La matematica è stata sfidata da brillanti scrittori in veste di eccentrici divulgatori. Hans Magnus Enzensberger (n.1929), sospettando che non sarebbe riuscito con argomenti ragionevoli a convincere un giovinetto sveglio di quanto la matematica sia facile e divertente, ha inventato un mago dei numeri pronto a insinuarsi nei suoi sogni (Il Mago dei Numeri, 1997). Presentandosi una notte nel sonno di Roberto, invece dei soliti pesci voraci e degli scivoli senza fine, chiarisce subito che “gran parte dei veri matematici i calcoli non li sanno nemmeno fare. Non vogliono sprecare il tempo…”. Lui preferisce spiegare i numeri infiniti dividendo un unico chewing-gum tra seicento miliardi di topi. Per cominciare. Ma servono allo scopo anche i moscerini, i funghi, le noci di cocco, i conigli e i gabbiani. E i numeri vestiti con squillanti magliette colorate interpretano i pari, i dispari ma anche i saltellati (22, 23, 24), i triangolari. Poi ci sono numeri che si mordono la coda e all’improvviso si mette a nevicare: i fiocchi di neve con la loro regolata difformità e il freddo intenso introducono un esercizio sui numeri irragionevoli e la sequenza di Bonaccione, dietro cui si nascondono il matematico pisano Leonardo Fibonacci (1175 c. – 1235c.) e la sua famosa successione in cui il rapporto tra coppie di termini tende al numero 1,61803, cioè alla sezione aurea. Di cui Paperino sa quasi tutto.
Il reverendo Edwin A. Abbott (1838-1926) ha romanzato la geometria (Flatland, 1884), inventando un mondo bidimensionale abitato da quadrati, triangoli, pentagoni, poligoni e circoli, organizzati in una società fortemente gerarchizzata e classista, dove l’incompiutezza e la marginalità delle donne è implicita nella loro forma di segmenti. I Triangoli avranno un carattere spigoloso e i Circoli saranno i più prossimi alla perfezione. Il brillante narratore è un Quadrato che esplorerà altri mondi, quello unidimensionale della Linea e quello tridimensionale guidato dalla virgiliana sapienza di una Sfera.


Lewis Carroll (1832-1898), l’autore di Alice nel paese della meraviglie, era un matematico cui non facevano difetto umorismo e ingegnosità. Giochi di parole, filastrocche surreali, indovinelli fulminei e sotterranei rompicapo, fioriscono ovunque nei suoi libri. Nel 1885 pubblicò un libretto intitolato A Tangled Tale (Una storia ingarbugliata) che raccoglieva dieci piccole vicende, ognuna un nodo del compiuto garbuglio, uscite a puntate cinque anni prima su “The Monty Packet”. In ciascuna storia, come una medicina nascosta con abilità ma con scarsi risultati nella marmellata del fanciullo, è nascosto un problema o più d’uno, di tipo aritmetico, algebrico o geometrico, per divertire ed eventualmente istruire il lettore. I titoli di ogni capitolo sono promettenti, anche se le difficoltà proposte sembrano più adatte a colti enigmisti: Matta Tematica, Un serpente con gli angoli, Pasticcini di Chelsea, ecc.
Nel primo capitolo, Excelsior, due turisti vestiti con cotta di maglia balzano giù da una rupe a sei miglia l’ora, preoccupati di raggiugere la locanda in tempo per la cena. Dopo rapidi scambi di battute infarciti di doppi sensi sulla fame di entrambi e il timore di trovare la tavola sparecchiata, uno dei due si domanda quante miglia avranno percorso sino alle nove, essendo partiti alle tre e avendo percorso tre miglia all’ora in salita e quattro in pianura. E quando sono arrivati in cima alla collina? Tutti i brevi racconti sono, come il primo, deliziosi, assurdi, con dialoghi che si vorrebbe ascoltare dalle voci di Totò e Peppino de Filippo: i problemi che pongono però, così complessi che persino le soluzioni mi hanno messo in difficoltà.

I due viaggiatori impazienti e impropriamente vestiti sono illustrati da Arthur B. Frost (1851-1928)
Carrol con la sua invocazione omerica sembra in ogni caso avere in mente un allievo se non alle prime, alle seconde armi.
Pupillo caro!
Da te con gran perizia dominate,
non soltanto le quattro operazioni
ma le radici cubiche e quadrate
fan fede alle tue certe cognizioni.Orsù procedi!
E di tua fama imperitura eco
possa nel tempo rinnovar la storia
così che sempre s’accompagni teco
più che al sommo Euclide eccelsa gloria.
(trad. Silvia Lalìa)
E anche quando Carrol sceglie la logica (Symbolic Logic, 1896) lo fa con tale strafottente arbitrarietà che i suoi esercizi potrebbero diventare il testo di un eccellente libro per l’infanzia: 1. Tutti i budini sono buoni. 2. Questo piatto è un budino. 3. Le cose buone non sono mai sane. Questo piatto non è sano. Oppure: 1. I maiali non sanno volare 2. I maiali sono ingordi. Ci sono degli ingordi che non sanno volare. E ancora: 1. Nessun imperatore fa il dentista. 2. Tutti dentisti sono temuti dai bambini. Alcune persone temute dai bambini non sono imperatori. (trad. Carla Muschio)
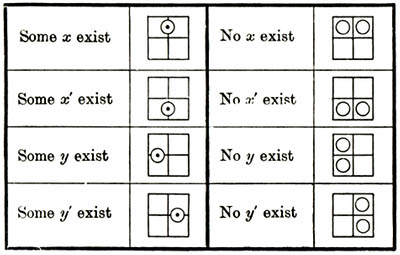
Alice nel paese dell’oscurità…
Nonostante le prescrizioni di Edgar Allan Poe, non ho sin qui proceduto passo dopo passo, né con rigida consequenzialità e forse per questo non so concludere se non ricominciando. Dunque vorrei innanzitutto che della matematica si insegnasse ai bambini (e, bambino, avrei voluto mi si facesse scoprire) l’incessante creatività, la struttura sostenuta dalle infinite variazioni e l’onnipresente ricchezza dell’analogia, quel così come… che nella Recherche di Marcel Proust, romanzo di mille corrispondenze quindi matematico suo malgrado, apre a continue rivelazioni, a incessanti trasformazioni e a sorprendenti rivoluzioni.





